In this work, we studied the effect of frequency and temperature on the optimal dimensions of a quantum well photodiode made of an alloy of materials (AlGaAs/GaAs). In fact, the derivative of the photocurrent density with respect to the recombination velocity at the junction (Sf) gives a quadratic equation whose solutions are expressions of the recombination velocities (Se1 and Se2) at the front surface. Thus, by analyzing the mathematical expressions describing the recombination rates of charge carriers in the solar cell, the graphical representation of these relationships based on different parameters, such as operating frequency and temperature, allows the optimal thickness to be precisely determined, maximizing energy conversion efficiency while minimizing recombination losses. Finally, analysis of these curves made it possible to establish calibration relationships for the optimal thickness, thus providing a reliable prediction of the solar cell's behavior and the material's efficiency. The calibration curves obtained provide a solid basis for studying system performance, optimizing manufacturing processes and adjusting production parameters. This approach improves the efficiency of quantum well solar cells through precise characterization, with the aim of maximizing their energy yield.
| Published in | Composite Materials (Volume 9, Issue 1) |
| DOI | 10.11648/j.cm.20250901.14 |
| Page(s) | 46-52 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Quantum Well Solar Cell, Recombination Speed, Optimal Thickness, Temperature and Frequency
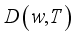 , temperature
, temperature 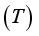
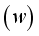
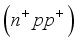 cell under monochromatic illumination in dynamic frequency regime for different temperatures.
cell under monochromatic illumination in dynamic frequency regime for different temperatures. 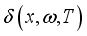 carriers in the dynamic frequency regime is given by the following relation (1):
carriers in the dynamic frequency regime is given by the following relation (1): 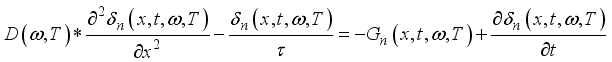 (1)
(1) 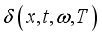 is the density of excess minority charge carriers which can be written in the form.
is the density of excess minority charge carriers which can be written in the form. 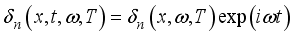
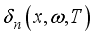 the spatial component and the temporal component.
the spatial component and the temporal component. 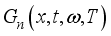 is the carrier generation
is the carrier generation 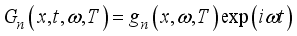
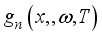 the spatial component
the spatial component 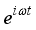 and the temporal component. We have:
and the temporal component. We have: 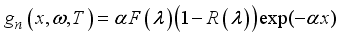
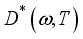 is the complex diffusion coefficient of excess minority carriers. Its expression is given by
is the complex diffusion coefficient of excess minority carriers. Its expression is given by 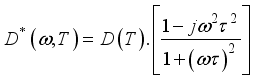
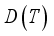 is the diffusion coefficient of the electron carriers given by the relation below:
is the diffusion coefficient of the electron carriers given by the relation below: 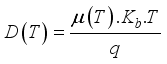
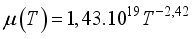 is the electron mobility coefficient
is the electron mobility coefficient 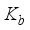 is the Boltzmann coefficient
is the Boltzmann coefficient 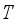 is the temperature
is the temperature 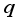 is the elementary charge of the electron
is the elementary charge of the electron 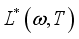 is the complex diffusion coefficient of the excess minority carriers is given by:
is the complex diffusion coefficient of the excess minority carriers is given by: 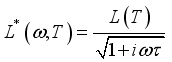
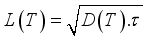 is the diffusion length of excess minority carriers.
is the diffusion length of excess minority carriers. 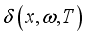 is of the form:
is of the form: 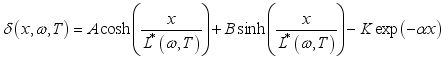 (2)
(2) 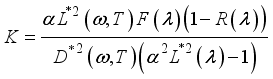
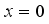
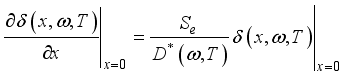 (3)
(3) 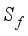 the speed of recombination of minority carriers on the front face.
the speed of recombination of minority carriers on the front face. 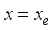
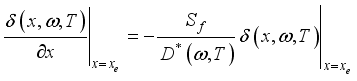 (4)
(4) 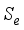 the recombination speed of minority carriers on the front side.
the recombination speed of minority carriers on the front side. 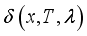 (2) which translates into the following relation:
(2) which translates into the following relation: 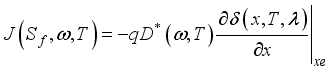 (5)
(5) 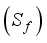 is zero:
is zero: 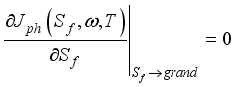 (6)
(6) 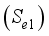 and
and 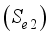 .
. 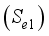 and
and 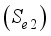 .
. 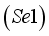 and
and 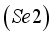 , gives the thickness of the solar cell emitter for each value of the low-frequency temperature. Thus, from these data, the table below is established:
, gives the thickness of the solar cell emitter for each value of the low-frequency temperature. Thus, from these data, the table below is established: Temperature (K) | Optimum thickness (Cm).10-4 |
|---|---|
300 | 9.689 |
340 | 8.919 |
380 | 8.483 |
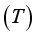 in kelvin and optimum thickness
in kelvin and optimum thickness 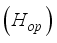 in
in 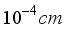 is given by the following formula:
is given by the following formula: 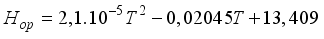
Temperature (K) | Optimum thickness (Cm).10-4 | |
|---|---|---|
300 | 8.407 | |
340 | 7.975 | |
380 | 7.710 |
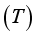 in Kelvin to the optimal thickness
in Kelvin to the optimal thickness 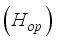 in
in 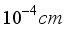 the material is expressed by a functional relationship of the following form:
the material is expressed by a functional relationship of the following form: 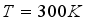 :
: Frequency (Hz) | Optimum thickness (Cm).10-3 |
|---|---|
1,75.102 | 1,026 |
2,75.104 | 1,024 |
3,75.106 | 0,5047 |
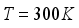 .
. 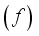 in Hz and optimum thickness
in Hz and optimum thickness 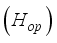 in cm is deduced from the results in Table 3.
in cm is deduced from the results in Table 3. 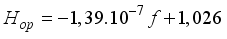
Frequency (Hz) | Optimum thickness (Cm).10-3 |
|---|---|
1,75.102 | 1,074 |
2,75.104 | 1,061 |
3,75.106 | 0,5213 |
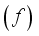 in Hz to the optimum thickness
in Hz to the optimum thickness 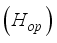 in cm, based on the data in Table 4, is as follows:
in cm, based on the data in Table 4, is as follows: 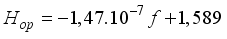
K | Kelvin |
Hop | Optimal Thickness |
Kb | Boltzmann Coefficient |
| [1] | Howard Geller, “Energy Revolution”, Renewable Energy World, 6/4, 34-49 (2003). |
| [2] | C. T. Sah, ‘High Efficiency Cristalline Silicon Solar Cells’ Solar Cells, 17, pp. 1-27, 1986. |
| [3] | J. R. Hauser and P. M. Dunbar, ‘Performance Limitations of Silicon Solar Cells’, IEEE Trans. on Elec. Devices ED-24, N°4, pp. 305-321, 1977. |
| [4] | WOODALL, J. M. and HOVEL, H. J., Appl. Phys. Lett. 30 (1977) 492. |
| [5] | SAHAI, R., EDWALL, D. D. and HARRIS, J. S. Jr., Appl. Phys. Lett. 34 (1979) 147. |
| [6] | S. Shao, H. et Lu, Temperature dependence of photovoltic cell efficiency: A reciew. Energy Reports, 2021, 7, 293-306. |
| [7] | B. Li, X. B. Xiang, Z. P. Y ou, Y. Xu, X. Y. Fei, X. B. Liao, High efficiency AlxGal_xAs/GaAs solarcells: Fabrication, irradiation and annealing effect, Sol. EnergyMater. Sol. Cells44(1996)63-67. |
| [8] | E. Gaubas and J. Vanhellemont, “A simple technique for the separation of bulk and surface recombination parameters in silicon,” J. Appl. Phys., vol. 80, no. 11, pp. 6293-6297, Dec. 1996, |
| [9] | J. M. Dorkel and P. Leturcq, “Carrier mobilities in silicon semi-empirically related to temperature, doping and injection level,” Solid. State. Electron., vol. 24, no. 9, pp. 821-825, Sep. 1981, |
| [10] | R. Mane et al., “Minority Carrier Diffusion Coefficient D*(B, T): Study in Temperature on a Silicon Solar Cell under Magnetic Field,” Energy Power Eng., vol. 9, no. 1, pp. 1-10, Jan. 2017, |
| [11] | S. Diouf et al., “Influence of Temperature and Frequency on Minority Carrier Diffusion Coefficient in a Silicon Solar Cell under Magnetic Field,” Energy Power Eng., vol. 11, no. 10, pp. 355-361, Oct. 2019, |
| [12] | A. Mandelis, “Coupled ac photocurrent and photothermal reflectance response theory of semiconducting p‐n junctions. I,” J. Appl. Phys., vol. 66, no. 11, pp. 5572-5583, Dec. 1989, |
| [13] | F. Ahmed and S. Garg, International Centre for Theoretical Physics (ICTP), Trieste, ITALY, Internal Report, Août 1986 |
| [14] | Andreas Mandelis J. Appl. Phys. Vol. 66 No. 11, 1 December, 1989, pp. 5572-5583. |
| [15] | M. F. M. Fall et al, « Vitesse de recombinaison de la surface arrière AC dans une cellule solaire en silicium n+-p-p+ sous une lumière et une température monochromatiques », J. Electromagn. Anal. Appl. vol. 13, n° 5, pp. 67-81, juil.2021, |
| [16] | D. Kabou et al., “AC BACK SURFACE RECOMBINATION IN N+-P-P+ SILICON SOLAR CELL: EFFECT OF TEMPERATURE,” Int. J. Adv. Res., vol. 8, no. 7, pp. 140-151, Jul. 2020, |
| [17] | C. H. Wang et A. Neugroschel, « Mesure de la durée de vie et de la vitesse de recombinaison de surface des porteurs minoritaires par photoluminescence dans le domaine fréquentiel», IEEE Trans. Electron Devices, vol. 38, n° 9, p. 2169-2180, 1991, |
| [18] | S. Gupta, F. Ahmed et S. Garg, « Une méthode pour la détermination des paramètres matériels τ, D, L0, S et a à partir du photocourant de court-circuit CA mesuré », Sol. Cells, vol. 25, n° 1, pp. 61-72, octobre 1988, |
| [19] | Arora, N. D. and Hauser, J. R. (1982) Temperature Dependence of Silicon Solar Cell Characteristics. Solar EnergyMaterials, 6,151-158. |
| [20] | Kunst, M. and Sanders, A. (1992) Transport of Excess Carriers in Silicon Wafers. Semiconductor Science and Technology, 7, 51-59. |
| [21] | Sissoko, G., Museruka, C., Corréa, A., Gaye, I. And Ndiaye, A. L. (1996), « Light Spectral Effect on Recombination Parameters of Silicon Solar Cell », World Renewable Energy Congress, Pergamon, Part III, pp. 1487-1490. |
| [22] | Diallo, H. L., Maiga, S. A., Wereme, A. and Sissoko, G. (2008), New Approach of Both Junction and Back Surface Recombination Velocities in a 3D Modelling Study of a PolycrystallineSilicon Solar Cell. The European Physical Journal Applied Physics, 42, 203-211. |
APA Style
Diallo, M. L., Ndiaye, P. G., Ndiaye, M., Kharma, G., Traore, P. T., et al. (2025). Effects of Frequency and Temperature on Optimum Dimensions of a Quantum Well Solar Cell (AlGaAs/GaAs). Composite Materials, 9(1), 46-52. https://doi.org/10.11648/j.cm.20250901.14
ACS Style
Diallo, M. L.; Ndiaye, P. G.; Ndiaye, M.; Kharma, G.; Traore, P. T., et al. Effects of Frequency and Temperature on Optimum Dimensions of a Quantum Well Solar Cell (AlGaAs/GaAs). Compos. Mater. 2025, 9(1), 46-52. doi: 10.11648/j.cm.20250901.14
@article{10.11648/j.cm.20250901.14,
author = {Mamadou Lamine Diallo and Papa Gueye Ndiaye and Mor Ndiaye and Gaye Kharma and Papa Touty Traore and Issa Diagne},
title = {Effects of Frequency and Temperature on Optimum Dimensions of a Quantum Well Solar Cell (AlGaAs/GaAs)
},
journal = {Composite Materials},
volume = {9},
number = {1},
pages = {46-52},
doi = {10.11648/j.cm.20250901.14},
url = {https://doi.org/10.11648/j.cm.20250901.14},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.cm.20250901.14},
abstract = {In this work, we studied the effect of frequency and temperature on the optimal dimensions of a quantum well photodiode made of an alloy of materials (AlGaAs/GaAs). In fact, the derivative of the photocurrent density with respect to the recombination velocity at the junction (Sf) gives a quadratic equation whose solutions are expressions of the recombination velocities (Se1 and Se2) at the front surface. Thus, by analyzing the mathematical expressions describing the recombination rates of charge carriers in the solar cell, the graphical representation of these relationships based on different parameters, such as operating frequency and temperature, allows the optimal thickness to be precisely determined, maximizing energy conversion efficiency while minimizing recombination losses. Finally, analysis of these curves made it possible to establish calibration relationships for the optimal thickness, thus providing a reliable prediction of the solar cell's behavior and the material's efficiency. The calibration curves obtained provide a solid basis for studying system performance, optimizing manufacturing processes and adjusting production parameters. This approach improves the efficiency of quantum well solar cells through precise characterization, with the aim of maximizing their energy yield.
},
year = {2025}
}
TY - JOUR T1 - Effects of Frequency and Temperature on Optimum Dimensions of a Quantum Well Solar Cell (AlGaAs/GaAs) AU - Mamadou Lamine Diallo AU - Papa Gueye Ndiaye AU - Mor Ndiaye AU - Gaye Kharma AU - Papa Touty Traore AU - Issa Diagne Y1 - 2025/06/30 PY - 2025 N1 - https://doi.org/10.11648/j.cm.20250901.14 DO - 10.11648/j.cm.20250901.14 T2 - Composite Materials JF - Composite Materials JO - Composite Materials SP - 46 EP - 52 PB - Science Publishing Group SN - 2994-7103 UR - https://doi.org/10.11648/j.cm.20250901.14 AB - In this work, we studied the effect of frequency and temperature on the optimal dimensions of a quantum well photodiode made of an alloy of materials (AlGaAs/GaAs). In fact, the derivative of the photocurrent density with respect to the recombination velocity at the junction (Sf) gives a quadratic equation whose solutions are expressions of the recombination velocities (Se1 and Se2) at the front surface. Thus, by analyzing the mathematical expressions describing the recombination rates of charge carriers in the solar cell, the graphical representation of these relationships based on different parameters, such as operating frequency and temperature, allows the optimal thickness to be precisely determined, maximizing energy conversion efficiency while minimizing recombination losses. Finally, analysis of these curves made it possible to establish calibration relationships for the optimal thickness, thus providing a reliable prediction of the solar cell's behavior and the material's efficiency. The calibration curves obtained provide a solid basis for studying system performance, optimizing manufacturing processes and adjusting production parameters. This approach improves the efficiency of quantum well solar cells through precise characterization, with the aim of maximizing their energy yield. VL - 9 IS - 1 ER -